Day 3: Calculate & Test
Today, the students posted their scales they came up with on the board. Next, they calculated how long the hallway was and posted their answers on the other board.
We then compared their calculated answers to the real hallway.
The hallway is measured at 479 ft.
Afterwords, I had students discuss why their numbers were off. Some answers included:
Below is how to convert:
To convert from either one unit to another or using the scale to either scale up or down, the process is the same. It's all a matter of ratio's. There are three methods to do this - and I'll discuss all three here.
Say I run a kennel and it just seems to work out that there has to be 3 dogs for every 2 cats. There is better peace and harmony when it's set up like this. So... here's the deal... I've got 18 dogs, how many cats must I have in order for there to be peace and harmony?
Below are the three ways to approach this problem.
Straight Ratio:
With the straight ratio approach, to find out how many cats I would need, you would first divide the total number of dogs by the amont of dogs you would need for the base ratio. In this case, it turns out that 18 dogs divided by 3 dogs gives us a multiple of 6.
Next, I simply multiply the top number by the same multiple. In other words, I would multiply 2 cats by 6 to find out how many cats I'd need. In this case, I'd need 12 cats if I had 18 dogs.
See how I did it below:
Today, the students posted their scales they came up with on the board. Next, they calculated how long the hallway was and posted their answers on the other board.
We then compared their calculated answers to the real hallway.
The hallway is measured at 479 ft.
Afterwords, I had students discuss why their numbers were off. Some answers included:
- Accuracy
- Measurement
- Mathematics and Calculation Difficulties
Below is how to convert:
To convert from either one unit to another or using the scale to either scale up or down, the process is the same. It's all a matter of ratio's. There are three methods to do this - and I'll discuss all three here.
Say I run a kennel and it just seems to work out that there has to be 3 dogs for every 2 cats. There is better peace and harmony when it's set up like this. So... here's the deal... I've got 18 dogs, how many cats must I have in order for there to be peace and harmony?
Below are the three ways to approach this problem.
Straight Ratio:
With the straight ratio approach, to find out how many cats I would need, you would first divide the total number of dogs by the amont of dogs you would need for the base ratio. In this case, it turns out that 18 dogs divided by 3 dogs gives us a multiple of 6.
Next, I simply multiply the top number by the same multiple. In other words, I would multiply 2 cats by 6 to find out how many cats I'd need. In this case, I'd need 12 cats if I had 18 dogs.
See how I did it below:
Fish Method:
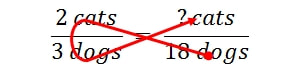
The fish method is a shortcut of the long hand algebra. The basic idea is to cross multiply and divide to find the final answer.
In the example below, you begin with the ratio that has the missing piece. In this case, it's the cats once again. So since we have the total number of dogs, but not cats, we start off with the dogs.
The fish method is a shortcut of the long hand algebra. The basic idea is to cross multiply and divide to find the final answer.
In the example below, you begin with the ratio that has the missing piece. In this case, it's the cats once again. So since we have the total number of dogs, but not cats, we start off with the dogs.
- Multiply the total no. of dogs with the ratio of the cats.
- Divide that answer with the ratio of the dogs
- Wala, you get a final answer of total cats.
Classic Conversion:
With classic conversions, you're converting based on a rate that is equal to each other. Kind of hard to explain - so bare with me.
Since we have 18 dogs, I know that for every 3 dogs I need 2 cats. So if I multiply the 18 dogs by the ratio of cats to dogs, then I can find out how many cats I need. However, it must be set up correctly.
I want to set it up so that the unit of "dogs" gets canceled out of the mathematical process. To do that, I need to set up the ratio where dogs is on the bottom. By setting up 2 cats per 3 dogs, the unit "dogs" get's canceled out, and we're left with cats.
Next, simply multiply everything in the numerator together and multiply everything in the denominator together, then finish off the calculation.
With classic conversions, you're converting based on a rate that is equal to each other. Kind of hard to explain - so bare with me.
Since we have 18 dogs, I know that for every 3 dogs I need 2 cats. So if I multiply the 18 dogs by the ratio of cats to dogs, then I can find out how many cats I need. However, it must be set up correctly.
I want to set it up so that the unit of "dogs" gets canceled out of the mathematical process. To do that, I need to set up the ratio where dogs is on the bottom. By setting up 2 cats per 3 dogs, the unit "dogs" get's canceled out, and we're left with cats.
Next, simply multiply everything in the numerator together and multiply everything in the denominator together, then finish off the calculation.
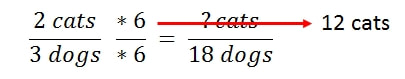

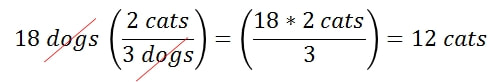
 RSS Feed
RSS Feed
